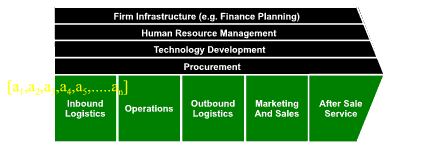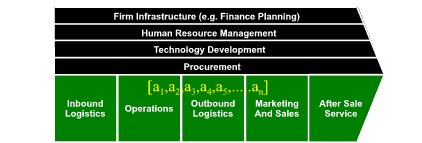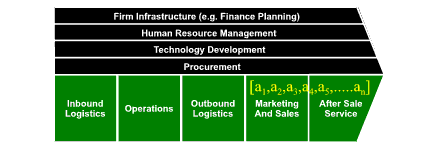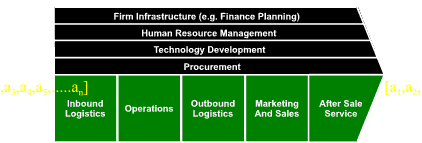
Ashby1 uses Shannon’s2 entropy measures in his derivation of the concept of Variety. By considering chains of symbols as Markov vectors (a chain of symbols in which the probability of each symbol is dependent on the value of the previous symbol), Ashby derives the Variety of various chains of symbols. He demonstrates that the variety of a particular Markov chain is directly proportional to its length, and that the total variety of a set of independent chains is the sum of the variety of the individual chains. He also shows that a Markov chain in which all symbol transitions are equally probable has the maximum possible variety.
Lind & Goldkuhl3 model business transactions as a series of exchanges, each exchange constructed from a sequence of business acts. A transaction can be characterised as a chain of business acts with the whole transaction considered a Markov chain. The variety in the transaction (and hence its information content) using Ashby’s measures of variety means that
- The total variety of a set of independent transactions is the sum of the variety in each transaction.
- The variety of an individual transaction is proportional to the length of the chain of related actions that constitute the transaction.
- The maximum variety in a chain of actions occurs when all possible action pairs are equiprobable.
The total variety in the set of transactions that occur within a business, and for which (according to Ashby’s law of requisite variety) the organisation requires sufficient capacity to absorb, is a function of
- The number of individual transactions. [Scale]
- The size of each transaction - as measured by the length of its sequence of actions. [Complexity]
- The diversity in the number of different ways in which the transactions can occur. [Diversity]
These three components are inherently independent characteristics (count, length, probability) of the Markov chains that represent the business transactions and can be treated as three dimensions of a Cartesian Information Space.
1 Ashby, W. R. (1956). An Introduction to Cybernetics, Chapman & Hall http://pcp.vub.ac.be/books/IntroCyb.pdf
2 Shannon, C. E. (1948). "A Mathematical Theory of Communication." The
Bell System Technical Journal Vol. 27(July, October, 1948.): pp. 379-423,623-656.
3 Lind, M. and Goldkuhl, G. (2001). Generic Layered Patterns for Business Modelling. Proceedings of the Sixth International
Workshop on the Language-Action
